Answer:
Correct choice: a. k = 13.5; xy = 13.5
Explanation:
Inverse Proportion
Two variables x and y are in inverse proportion or variation if:
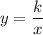
Where k is the constant of proportionality
Since we know that y=4.5 when x=3:
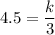
Solving for k:

Thus the equation is:
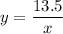
Or, equivalently:
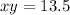
Correct choice: a. k = 13.5; xy = 13.5