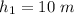Answer:
a
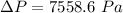
b
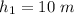
Step-by-step explanation:
From the question we are told that
The position of the column of mercury in the barometer is
 \
\
The density of mercury is
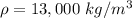
Generally the pressure of the atmosphere at that column is mathematically represented as
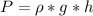
=>

=>
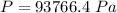
Generally the atmospheric pressure at sea level (Generally the pressure before the change in level of the mercury column) is
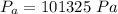
Generally the change in air pressure is mathematically represented as
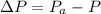
=>
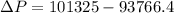
=>
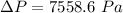
Generally the height which the column will rise to is mathematically evaluated as
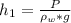
Here
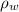 is the density of water with value
is the density of water with value
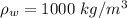
So
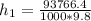
=>