Answer:
Explicación más abajo
Explanation:
Integración Indefinida
La integral
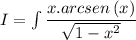
Se resuelve con el cambio de variables:
t=arcsen(x)
Una vez hechos los cambios, la integral se resuelve en función de t:
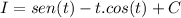
Hay que devolver los cambios para mostrarla en función de x.
El cambio de variables también se puede escribir:
x=sen(t)
Recordando que
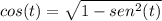
Entonces:
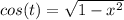
Devolviendo los cambios:
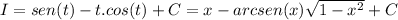
Es la respuesta correcta