Answer:
W = 11,416.6879 N
L ≈ 64.417 cm
Step-by-step explanation:
The maximum shear stress,
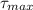 , is given by the following formula;
, is given by the following formula;
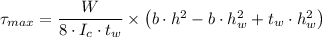
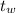 = 1 cm = 0.01
= 1 cm = 0.01
h = 29 cm = 0.29 m
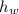 = 25 cm = 0.25 m
= 25 cm = 0.25 m
b = 15 cm = 0.15 m
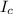 = The centroidal moment of inertia
= The centroidal moment of inertia
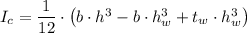
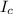 = 1/12*(0.15*0.29^3 - 0.15*0.25^3 + 0.01*0.25^3) = 1.2257083 × 10⁻⁴ m⁴
= 1/12*(0.15*0.29^3 - 0.15*0.25^3 + 0.01*0.25^3) = 1.2257083 × 10⁻⁴ m⁴
Substituting the known values gives;
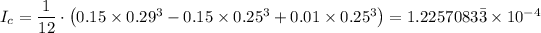
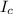 = 1.2257083
= 1.2257083
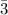 × 10⁻⁴ m⁴
× 10⁻⁴ m⁴
From which we have;
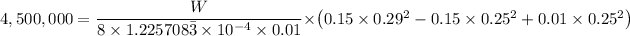
Which gives;
W = 11,416.6879 N
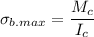
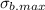 = 1500 N/cm² = 15,000,000 N/m²
= 1500 N/cm² = 15,000,000 N/m²
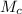 = 15,000,000 × 1.2257083 × 10⁻⁴ ≈ 1838.56245 N·m²
= 15,000,000 × 1.2257083 × 10⁻⁴ ≈ 1838.56245 N·m²
From Which we have;
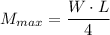
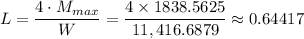
L ≈ 0.64417 m ≈ 64.417 cm.