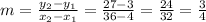Question

A school conducts 27 tests in 36 weeks. Assume the school conducts tests at a constant rate. What is the slope of the line that represents the number of tests on the y-axis and the time in weeks on the x-axis?

Answer 1

The slope is equal to
`(3)/(4)`.

Explanation:

In order to solve this question we need to know that.......

`m = (y_(2)-y_(1) )/(x_(2) - x_(1) )`

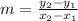
Where "m" = slope,"
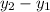`y_(2)-y_(1)`" = first difference, and
`x_(2) - x_(1)` is the difference of the x values of the two points that we chose to fid the slope.

(If you don't understand something I would recommend to read about first differences and how we can use the first differences to find the slope).

Now we need to find two points on the line. One of them is already given to us and it is (36,27). In order to find the second one we will have to find a point with "x" and "y" values that have the same relation ship to each other as the point (36,27). We can do that by doing the following

`(x/a)/(y/a) =(x_(1) )/(y_(1) )`

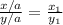
In this case a any common factor of "x" and "y" except 1. So now we can do the following...

`(36)/(27) = (36/9)/(27/9) = (4)/(3)`

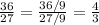
Now we know that another point on this line is (4,3).

Now all we have to imagine (36,27) as (
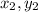`x_(2) ,y_(2)`), and imagine (4,3) as
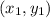`(x_(1) , y_(1))`. so now......

`m = (y_(2)-y_(1) )/(x_(2) - x_(1) ) = (27 - 3)/(36-4) = (24)/(32) = (3)/(4)`