Answer:
Angular displacement=68.25 rad
Step-by-step explanation:
Circular Motion
If the angular speed varies from ωo to ωf in a time t, then the angular acceleration is given by:
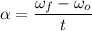
The angular displacement is given by:
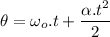
The wheel decelerates from ωo=13.5 rad/s to ωf=6 rad/s in t=7 s, thus:
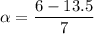
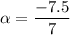
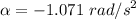
Thus, the angular displacement is:
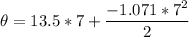
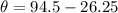
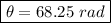
Angular displacement=68.25 rad