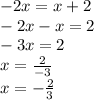Question

How to solve

`√(4) x {}^(2) = x + 2`
​

Answer 1

➩
`x=2,-(2)/(3)`

Explanation:

`√(4x^2)=x+2`

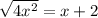
➨ We can also solve by completing both squares, however. Since we can pull out the square root.

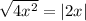`√(4x^2)=|2x|` ➩ Define of Absolute Value/Square Root

➩
`√(x^2)=|x|`

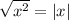
Thus, our new equation is ➩
`|2x|=x+2`

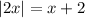
To solve an absolute-value equation, let there be two conditions.

➨ Where x ≥ 0

`2x=x+2\\`

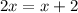
Move x to another side

`2x-x=2\\x=2`

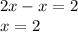
➨ Where x < 0

`-2x=x+2\\-2x-x=2\\-3x=2\\x=(2)/(-3)\\x=-(2)/(3)`