Answer:
See below for Part A.
Part B)

Explanation:
Part A)
The parabola given by the equation:
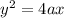
From 0 to h is revolved about the x-axis.
We can take the principal square root of both sides to acquire our function:

Please refer to the attachment below for the sketch.
The area of a surface of revolution is given by:
![\displaystyle S=2\pi\int_(a)^(b)r(x)√(1+\big[f^\prime(x)]^2) \,dx](https://img.qammunity.org/2021/formulas/mathematics/college/ikwm9d9dgg0pz8eh1b0dx89uuldm59s6wy.png)
Where r(x) is the distance between f and the axis of revolution.
From the sketch, we can see that the distance between f and the AoR is simply our equation y. Hence:
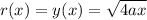
Now, we will need to find f’(x). We know that:
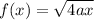
Then by the chain rule, f’(x) is:
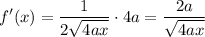
For our limits of integration, we are going from 0 to h.
Hence, our integral becomes:
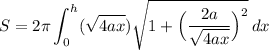
Simplify:

Combine roots;
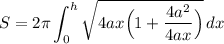
Simplify:
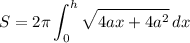
Integrate. We can consider using u-substitution. We will let:
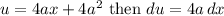
We also need to change our limits of integration. So:
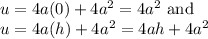
Hence, our new integral is:
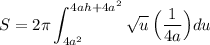
Simplify and integrate:
![\displaystyle S=(\pi)/(2a)\Big[\,(2)/(3)u^{(3)/(2)}\Big|^(4ah+4a^2)_(4a^2)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/znrqi4btn0j9xdckhxljghqv22bjnv9qbh.png)
Simplify:
![\displaystyle S=(\pi)/(3a)\Big[\, u^(3)/(2)\Big|^(4ah+4a^2)_(4a^2)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/qr15n63dvtm2oimp79wismn5nwwok5utsa.png)
FTC:
![\displaystyle S=(\pi)/(3a)\Big[(4ah+4a^2)^(3)/(2)-(4a^2)^(3)/(2)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/l1dm7bduxh6b3n4bkvs7k7rfnzmq1tt5b4.png)
Simplify each term. For the first term, we have:
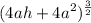
We can factor out the 4a:
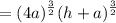
Simplify:
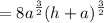
For the second term, we have:
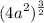
Simplify:
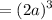
Hence:
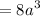
Thus, our equation becomes:
![\displaystyle S=(\pi)/(3a)\Big[8a^(3)/(2)(h+a)^(3)/(2)-8a^3\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/bogwf1sjo004535n59uzi9kymat6dt98to.png)
We can factor out an 8a^(3/2). Hence:
![\displaystyle S=(\pi)/(3a)(8a^(3)/(2))\Big[(h+a)^(3)/(2)-a^(3)/(2)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/su5cti572aadke08w8cpz21r511e2dauyj.png)
Simplify:
![\displaystyle S=(8\pi)/(3)√(a)\Big[(h+a)^(3)/(2)-a^(3)/(2)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/o8mhif6g7hkuezgyxvhtumeeddh1eph5q5.png)
Hence, we have verified the surface area generated by the function.
Part B)
We have:
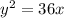
We can rewrite this as:
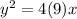
Hence, a=9.
The surface area is 1000. So, S=1000.
Therefore, with our equation:
![\displaystyle S=(8\pi)/(3)√(a)\Big[(h+a)^(3)/(2)-a^(3)/(2)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/o8mhif6g7hkuezgyxvhtumeeddh1eph5q5.png)
We can write:
![\displaystyle 1000=(8\pi)/(3)√(9)\Big[(h+9)^(3)/(2)-9^(3)/(2)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/mfbuwc96knuvnhdrme68y4wzqj9pe5k412.png)
Solve for h. Simplify:
![\displaystyle 1000=8\pi\Big[(h+9)^(3)/(2)-27\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/yml1dh4rd7h6ejrtcgxobp3lk3j5ugg841.png)
Divide both sides by 8π:
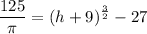
Isolate term:
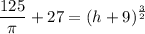
Raise both sides to 2/3:

Hence, the value of h is:
