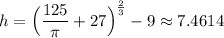Question

The portion of the parabola y²=4ax above the x-axis, where is form 0 to h is revolved about the x-axis. Show that the surface area generated is

A=8/3π√a[(h+a)³/²-a³/2]
Use the result to find the value of h if the parabola y²=36x when revolved about the x-axis is to have surface area 1000.​

Answer 1

You seem to have left out that 0 ≤ x ≤ h.

From y² = 4ax, we get that the top half of the parabola (the part that lies in the first quadrant above the x-axis) is given by y = √(4ax) = 2√(ax). Then the area of the surface obtained by revolving this curve between x = 0 and x = h about the x-axis is

`2\pi\displaystyle\int_0^h y(x) \sqrt{1+\left((\mathrm dy(x))/(\mathrm dx)\right)^2}\,\mathrm dx`

We have

y(x) = 2√(ax) → y'(x) = 2 • a/(2√(ax)) = √(a/x)

so the integral is

`4\sqrt a\pi\displaystyle\int_0^h \sqrt x √(1+\frac ax)\,\mathrm dx`

`=\displaystyle4\sqrt a\pi\int_0^h (x+a)^(\frac12)\,\mathrm dx`

`=4\sqrt a\pi\left[\frac23(x+a)^(\frac32)\right]_0^h`

`=\frac{8\pi\sqrt a}3\left((h+a)^(\frac32)-a^(\frac32)\right)`

Now, if y² = 36x, then a = 9. So if the area is 1000, solve for h :

`1000=8\pi\left((h+9)^(\frac32)-27\right)`

`\frac{125}\pi=(h+9)^(\frac32)-27`

`\frac{125+27\pi}\pi=(h+9)^(\frac32)`

`\left(\frac{125+27\pi}\pi\right)^(\frac23)=h+9`

`\boxed{h=\left(\frac{125+27\pi}\pi\right)^(\frac23)-9}`

Answer 2

See below for Part A.

Part B)

`\displaystyle h=\Big((125)/(\pi)+27\Big)^(2)/(3)-9\approx7.4614`

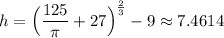
Explanation:

Part A)

The parabola given by the equation:

`y^2=4ax`

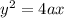
From 0 to h is revolved about the x-axis.

We can take the principal square root of both sides to acquire our function:

`y=f(x)=√(4ax)`

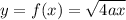
Please refer to the attachment below for the sketch.

The area of a surface of revolution is given by:

`\displaystyle S=2\pi\int_(a)^(b)r(x)√(1+\big[f^\prime(x)]^2) \,dx`

Where r(x) is the distance between f and the axis of revolution.

From the sketch, we can see that the distance between f and the AoR is simply our equation y. Hence:

`r(x)=y(x)=√(4ax)`

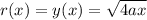
Now, we will need to find f’(x). We know that:

`f(x)=√(4ax)`

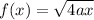
Then by the chain rule, f’(x) is:

`\displaystyle f^\prime(x)=(1)/(2√(4ax))\cdot4a=(2a)/(√(4ax))`

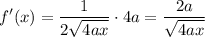
For our limits of integration, we are going from 0 to h.

Hence, our integral becomes:

`\displaystyle S=2\pi\int_(0)^(h)(√(4ax))\sqrt{1+\Big((2a)/(√(4ax))\Big)^2}\, dx`

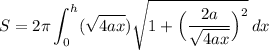
Simplify:

`\displaystyle S=2\pi\int_(0)^(h)√(4ax)\Big(\sqrt{1+(4a^2)/(4ax)}\Big)\,dx`

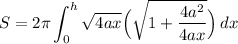
Combine roots;

`\displaystyle S=2\pi\int_(0)^(h)\sqrt{4ax\Big(1+(4a^2)/(4ax)\Big)}\,dx`

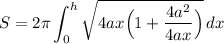
Simplify:

`\displaystyle S=2\pi\int_(0)^(h)√(4ax+4a^2)\, dx`

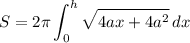
Integrate. We can consider using u-substitution. We will let:

`u=4ax+4a^2\text{ then } du=4a\, dx`

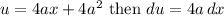
We also need to change our limits of integration. So:

`u=4a(0)+4a^2=4a^2\text{ and } \\ u=4a(h)+4a^2=4ah+4a^2`

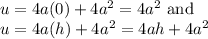
Hence, our new integral is:

`\displaystyle S=2\pi\int_(4a^2)^(4ah+4a^2)√(u)\, \Big((1)/(4a)\Big)du`

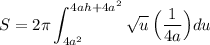
Simplify and integrate:

`\displaystyle S=(\pi)/(2a)\Big[\,(2)/(3)u^{(3)/(2)}\Big|^(4ah+4a^2)_(4a^2)\Big]`

Simplify:

`\displaystyle S=(\pi)/(3a)\Big[\, u^(3)/(2)\Big|^(4ah+4a^2)_(4a^2)\Big]`

FTC:

`\displaystyle S=(\pi)/(3a)\Big[(4ah+4a^2)^(3)/(2)-(4a^2)^(3)/(2)\Big]`

Simplify each term. For the first term, we have:

`\displaystyle (4ah+4a^2)^(3)/(2)`

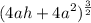
We can factor out the 4a:

`\displaystyle =(4a)^(3)/(2)(h+a)^(3)/(2)`

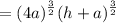
Simplify:

`\displaystyle =8a^(3)/(2)(h+a)^(3)/(2)`

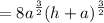
For the second term, we have:

`\displaystyle (4a^2)^(3)/(2)`

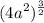
Simplify:

`\displaystyle =(2a)^3`

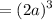
Hence:

`\displaystyle =8a^3`

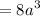
Thus, our equation becomes:

`\displaystyle S=(\pi)/(3a)\Big[8a^(3)/(2)(h+a)^(3)/(2)-8a^3\Big]`

We can factor out an 8a^(3/2). Hence:

`\displaystyle S=(\pi)/(3a)(8a^(3)/(2))\Big[(h+a)^(3)/(2)-a^(3)/(2)\Big]`

Simplify:

`\displaystyle S=(8\pi)/(3)√(a)\Big[(h+a)^(3)/(2)-a^(3)/(2)\Big]`

Hence, we have verified the surface area generated by the function.

Part B)

We have:

`y^2=36x`

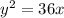
We can rewrite this as:

`y^2=4(9)x`

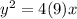
Hence, a=9.

The surface area is 1000. So, S=1000.

Therefore, with our equation:

`\displaystyle S=(8\pi)/(3)√(a)\Big[(h+a)^(3)/(2)-a^(3)/(2)\Big]`

We can write:

`\displaystyle 1000=(8\pi)/(3)√(9)\Big[(h+9)^(3)/(2)-9^(3)/(2)\Big]`

Solve for h. Simplify:

`\displaystyle 1000=8\pi\Big[(h+9)^(3)/(2)-27\Big]`

Divide both sides by 8π:

`\displaystyle (125)/(\pi)=(h+9)^(3)/(2)-27`

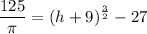
Isolate term:

`\displaystyle (125)/(\pi)+27=(h+9)^(3)/(2)`

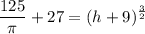
Raise both sides to 2/3:

`\displaystyle \Big((125)/(\pi)+27\Big)^(2)/(3)=h+9`

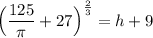
Hence, the value of h is:

`\displaystyle h=\Big((125)/(\pi)+27\Big)^(2)/(3)-9\approx7.4614`