Question

A person places $7320 in an investment account earning an annual rate of 8.2%,

compounded continuously. Using the formula V = Pert, where Vis the value of the
account in t years, P is the principal initially invested, e is the base of a natural
logarithm, and r is the rate of interest, determine the amount of money, to the
nearest cent, in the account after 12 years.

Answer 1

The amount of money after 12 years is $19581.99 to the nearest cents

Explanation:

The formula of the compound continuously interest is V = P
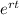`e^(rt)` , where

• V is the value of the account in t years

• P is the principal initially invested

• e is the base of a natural logarithm

• r is the rate of interest in decimal

∵ A person places $7320 in an investment account

∴ P = 7320

∵ The account earning an annual rate of 8.2%, compounded continuously

∴ r = 8.2% ⇒ divide it by 100 to change it to decimal

∴ r = 8.2 ÷ 100 = 0.082

∵ The time is 12 years

∴ t = 12

→ Substitute these values in the formula above to find V

∵ V = 7320
`e^(0.082(12))`

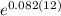
∴ V = 19581.99121 dollars

→ Round it to the nearest cents ⇒ 2 d.p

∴ V = 19581.99 dollars

∴ The amount of money after 12 years is $19581.99 to the nearest cents.