Answer:
⇨ Choice A.
Explanation:
We'll consider three choices and compare the answers with the given number line and points.
⟺ Choice A
This is the correct answer and here is why.
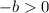
Solving Inequality is similar to solving equation. The difference is if the coefficient for the variable is in negative, moving to another side would swap the sign/operator of Inequality.
Thus, our new Inequality would be
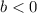 which is true by the number line itself.
which is true by the number line itself.
⟺ Choice B
The reason why choice B is not correct because the point a is lesser than the point b. It's obvious that point a cannot be greater than point b.
⟺ Choice C
The reason why choice C is not correct because if we solve the Inequality.
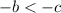
We can either solve for b-term or c-term, the outcome would be the same. I'll solve for both terms.
⇨ Solve for b-term
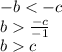
Also remember that moving a negative coefficient would swap the sign/operator of Inequality.
⇨ Solve for c-term
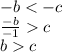
As b>c is not true in the number line. We notice that c point is greater than b point.
Thus, the clear answer is A choice.