Question

QUESTION 1

a)
1) A circular coil with radius 20 cm is placed with it's plane parallel and between two straight
wires P and Q. The coil carries current Icoil = 0.5A . Icoil is in clockwise direction when viewed
from left side. Wire P is located 40 cm to the left of a circular coil and carries current Ip = 0.2A
while wire Q is located 80 cm to the right of the circular coil and carries current lo =0.6A. Both
Ip and IQ are in the same directions into the paper. Determine the resultant of magnetic field at
the centre of a circular coil from the top view.
[7 marks]​

Answer 1

Magnetic field at the centre due to
`$I_P$` :

`$B_1 = (\mu_0 I_P)/(2 \pi d)$`

`$B_1 = (4 \pi * 10^(-7) * 0.2)/(2 \pi d)$`

`$B_1 =10^(-7) \ T$`

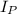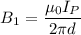
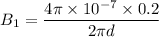
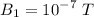
Its direction will be downwards in the plane of the paper.

Magnetic field at the centre due to
`$I_Q$` :

`$B_2 = (\mu_0 I_Q)/(2 \pi d)$`

`$B_2 = (4 \pi * 10^(-7) * 0.6)/(2 \pi * 0.8)$`

`$B_2 =1.5 * 10^(-7) \ T$`

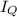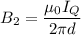
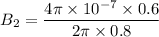
Its direction will be upwards in the plane of the paper

Magnetic field due to the coil:

`$B_3 = (\mu_0 I_(coil))/(2 r)$`

`$B_3 = (4 \pi * 10^(-7) * 0.5)/(2 * 0.2)$`

`$B_3 =3.14 * 10^(-7) \ T$`

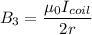
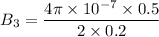
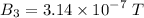
Its direction will be rightwards.

Now the resultant of the magnetic field at the centre.

`$B_(net) = √((B_2 -B_1)^2+B^2_3)$`

`$B_(net) = \sqrt{(0.5 * 10^(-7))^2+(3.14 * 10^(-7))^2}$`

`$B_(net) = 3.18 * 10^(-7) \ T$`

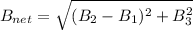
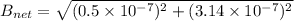
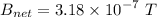
Now the direction ,

`$\tan \theta = (B_2-B_1)/(B_3)$`

`$\tan \theta = (0.5 * 10^(-7))/(3.14 * 10^(-7))$`

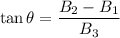
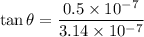
Therefore
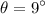`$\theta = 9^\circ$` (from right to upward)