Solution :
Magnetic field at the centre due to
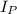 :
:
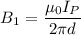
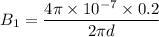
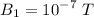
Its direction will be downwards in the plane of the paper.
Magnetic field at the centre due to
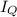 :
:
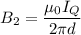
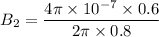
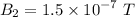
Its direction will be upwards in the plane of the paper
Magnetic field due to the coil:
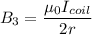
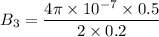
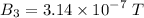
Its direction will be rightwards.
Now the resultant of the magnetic field at the centre.
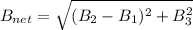
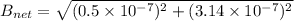
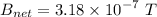
Now the direction ,
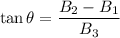
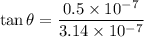
Therefore
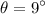 (from right to upward)
(from right to upward)