Question

Integrate each of the following 12 - lnx​

Answer 1

`\displaystyle \int {(12 - lnx)} \, dx = x[13 - ln(x)] + C`

General Formulas and Concepts:

Algebra I

• Terms/Coefficients
• Factoring

Calculus

Differentiation

• Derivatives
• Derivative Notation

Integration

• Integrals
• Indefinite Integrals
• Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

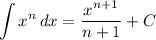
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

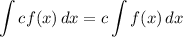
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

U-Substitution

• U-Solve

Integration by Parts:
`\displaystyle \int {u} \, dv = uv - \int {v} \, du`

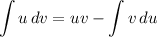
• [IBP] LIPET: Logs, inverses, Polynomials, Exponentials, Trig

Explanation:

Step 1: Define

Identify

`\displaystyle \int {(12 - lnx)} \, dx`

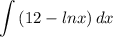
Step 2: Integrate Pt. 1

1. [Integral] Rewrite [Integration Property - Addition/Subtraction]:
   `\displaystyle \int {(12 - lnx)} \, dx = \int {12} \, dx - \int {lnx} \, dx`
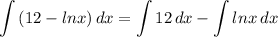
2. [1st Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {(12 - lnx)} \, dx = 12\int {} \, dx - \int {lnx} \, dx`
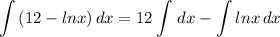
3. [1st Integral] Reverse Power Rule:
   `\displaystyle \int {(12 - lnx)} \, dx = 12x - \int {lnx} \, dx`

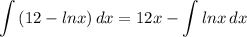
Step 3: Integrate Pt. 2

Identify variables for integration by parts using LIPET.

1. Set u:
   `\displaystyle u = lnx`
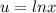
2. [u] Differentiate [Logarithmic Differentiation]:
   `\displaystyle du = (1)/(x) \ dx`
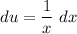
3. Set dv:
   `\displaystyle dv = dx`
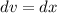
4. [dv] Integration Rule [Reverse Power Rule]:
   `\displaystyle v = x`

Step 4: Integrate Pt. 3

1. [Integral] Integration by Parts:
   `\displaystyle \int {(12 - lnx)} \, dx = 12x - \bigg[ xlnx - \int { \bigg( x \cdot (1)/(x) \bigg) } \, dx \bigg]`
2. [Integrand] Simplify:
   `\displaystyle \int {(12 - lnx)} \, dx = 12x - \bigg[ xlnx - \int {} \, dx \bigg]`
3. [Integral] Reverse Power Rule:
   `\displaystyle \int {(12 - lnx)} \, dx = 12x - \bigg[ xlnx - x + C \bigg]`
4. Simplify:
   `\displaystyle \int {(12 - lnx)} \, dx = 12x - xlnx + x + C`
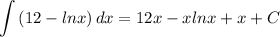
5. Factor:
   `\displaystyle \int {(12 - lnx)} \, dx = x[12 - ln(x) + 1] + C`
6. Simplify:
   `\displaystyle \int {(12 - lnx)} \, dx = x[13 - ln(x)] + C`

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Book: College Calculus 10e