Question

A wastewater treatment plant has a treatment capacity of 5000 m3/d with the average BOD of 150 mg/L, average total N of 40 mg/L, and average TSS of 350 mg/L in the primary settled effluent. The wastewater treatment process consists of primary settling, aeration tanks, secondary settling, and disinfection. The total suspended solid (TSS) in aeration tanks is 3500 mg/L. The settled sludge in the secondary settling tank is 10000 mg/L. The effluent regulation:

BOD<10 mg/L, N<5 mg/L, and TSS<50 mg/L.
Calculation requirement:
1) Assume HRT in aeration tanks is 4 hrs, and the waste sludge flow rate from secondary settling tanks is 500 m3/d. Calculate the F: M ratio and SRT.
2) Discuss whether this system can achieve good BOD removal or N removal.
3) If you are asked to prolong SRT to 25 days, which engineering parameter you can adjust in this wastewater treatment system? Recalculate the Question (1) to make sure SRT is longer than 25 days.

Answer 1

Following are the solution to the given points:

Step-by-step explanation:

`Q= 5000 (m^3)/(day)\\\\ Y_i= 150 (mg)/(L)\\\\TSS = 350 (mg)/(L)\\\\xi=3500 (mg)/(l) \\\\D_t(HRT) = 4 \ hrs\\\\Q_w = 500 (m^3)/(day)`

`tank \ volume = Q * D_t(HRT)`

`= 500 * (4)/(24)\\\\= 833.33 m^3`

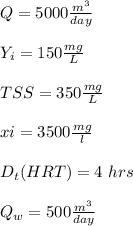
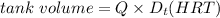
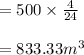
In point 1:

`(F)/(M) = (Q \ Y_i)/(Q \ x_i) \\\\`

`= (5000 * 150 * 10^3)/(833.33 * 3500 * 10^3)\\\\= 0.257`

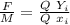
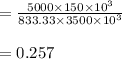
Calculating (SRT):

`= (V X_i)/(Q_w \ x_w) \\\\\to x_w` not defined

`= 350 \ (mg)/(l)\\\\= (833.33 * 3500)/(500 * 350)\\\\= 16.67 \ days`

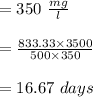
In point 2:

The regulated values now are less than the tank entry

In point 3:

`\to SRT= 25 = (V \ X_i)/( Q_w \ X_w)\\\\\to Q_w \ X_w = (833.33 * 3500 )/(25)`

`= 116666.2 * 10^3 \ (mg)/(day)\\\\= 116.662 * 10^3 \ (mg)/(day)`

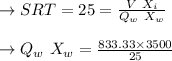
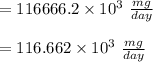
Here the volume is fixed hence
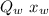`Q_w \ x_w` must be changed.