Answer: 0.038528
Explanation:
Given: Sample size : n= 50
Population proportion: p = 80% = 0.80
Let x be the random variable .
Mean
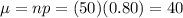
Standard deviation
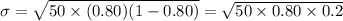
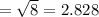
The probability that fewer than 35 of the sampled will be infected =
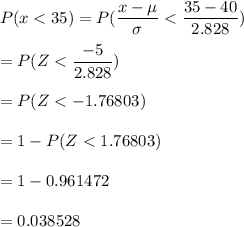
Hence, the required probability = 0.038528