Answer:

Step-by-step explanation:
We are given the reaction:
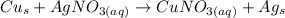
We know that there are 25 grams of silver nitrate, or AgNO₃. First, we must find the molar mass of silver nitrate.
Silver Nitrate (AgNO₃)
Identify the molar masses of each element in silver nitrate using the Peirodic Table.
- Silver (Ag): 107.868 g/mol
- Nitrogen (N) : 14.007 g/mol
- Oxygen (O): 15.999 g/mol
Next, calculate the molar mass. There is a subscript of 3 after the O, so we must multiply oxygen's molar mass by 3.
- O₃= (15.999 g/mol) *3=49.997 g/mol
AgNO₃= (107.868 g/mol) + (14.007 g/mol)+(49.997 g/mol)=169.872 g/mol
Silver
Next, use stoichometry to find the mass of the silver.
- Convert grams of silver nitrate to moles.
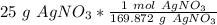
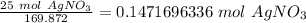
In this reaction, 1 mole of silver nitrate yields 1 mole of silver.
2. Convert moles of silver nitrate to moles of silver.
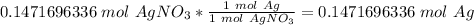
We know that silver's molar mass is 107.868 grams per mole.
3. Convert moles of silver to grams of silver.
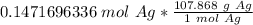
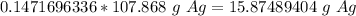
4. Round
The original measurement given had 2 siginficant figures (25= 2 and 5). Therefore, we must round to 2 sig figs or the nearest whole number for this problem.
The 8 in the tenth place tells us to round up to the nearest whole number.
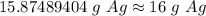
About 16 grams of silver would be produced.