Question

What is the 21st term of the sequence with a1 = -6 and d = 4?

choices-
74

70

78

-40

Answer 1

SoluTion :-

Here we will use the formula

`\tt \: a_n \: = a_1 +( n - 1)\: * d`

`\tt\: a_(21) = −6+(21−1)4`

By using PEMDAS

`\tt \: a_(21) = - 6 + (20)4`

`\tt \: a_(21) \: = - 6 + 80 = 74`

`\huge \tt \bigodot \: \: 74`

Answer 2

`\boxed {\boxed {\sf 74}}`

Explanation:

The nth term of an arithmetic sequence can be found using the following formula.

`a_n=a_1+(n-1)d`

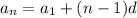
Where n is the term, a₁ is the first term, and d is the common difference.

We want to find the 21st term, we know the first term is -6, and the common difference is 4.

`n= 21\\a_1= -6 \\d=4`

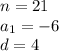
Substitute the values into the formula.

`a_(21)=-6+(21-1)4`

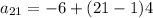
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.

Solve inside the parentheses.

`a_(21)=-6+(20)4`

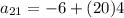
Multiply 20 and 4.

`a_(21)= -6+80 \\`

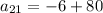
Add -6 and 80.

`a_(21)=74`

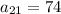
The 21st term of the sequence is 74