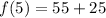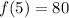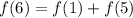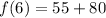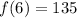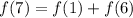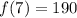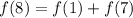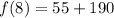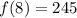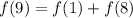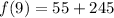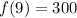Answer:
8. Arithmetic Progression
9.
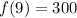
Explanation:
Given
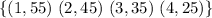
Solving (8): Arithmetic or Geometric
We start by checking if it is arithmetic by checking for common difference (d).
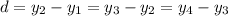
This gives:
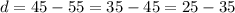
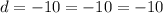
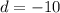
Because the common difference is equal, then it is an arithmetic progression
Solving (8):
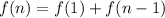
To find f(9), we substitute 9 for n

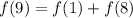
We need to solve for f(8); substitute 8 for n

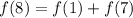
We need to solve for f(7); substitute 7 for n

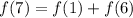
We need to solve for f(6); substitute 6 for n
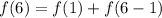
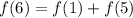
We need to solve for f(5); substitute 6 for n
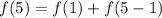
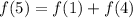
From the function, f(4) = 25 and f(1) = 55.
So: