Answer:
Explanation:
Given that:
The equation of the damped vibrating spring is y" + by' +2y = 0
(a) To convert this 2nd order equation to a system of two first-order equations;
let y₁ = y
y'₁ = y' = y₂
So;
y'₂ = y"₁ = -2y₁ -by₂
Thus; the system of the two first-order equation is:
y₁' = y₂
y₂' = -2y₁ - by₂
(b)
The eigenvalue of the system in terms of b is:
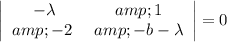
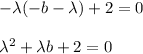
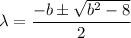
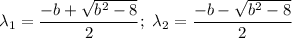
(c)
Suppose
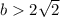 , then λ₂ < 0 and λ₁ < 0. Thus, the node is stable at equilibrium.
, then λ₂ < 0 and λ₁ < 0. Thus, the node is stable at equilibrium.
(d)
From λ² + λb + 2 = 0
If b = 3; we get
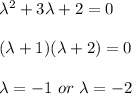
Now, the eigenvector relating to λ = -1 be:
![v = \left[\begin{array}{ccc}+1&1\\-2&-2\\\end{array}\right] \left[\begin{array}{c}v_1\\v_2\\\end{array}\right] = \left[\begin{array}{c}0\\0\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/qtnxjezr4zeut7ikjdiym8hhpbz0pbnul3.png)
![\sim v = \left[\begin{array}{ccc}1&1\\0&0\\\end{array}\right] \left[\begin{array}{c}v_1\\v_2\\\end{array}\right] = \left[\begin{array}{c}0\\0\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/zur4x5tgfgeirfb8th28h4amfodbedg238.png)
Let v₂ = 1, v₁ = -1
![v = \left[\begin{array}{c}-1\\1\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/ytv4pnoldmwiv3ns9us52d7b34ii3n9e83.png)
Let Eigenvector relating to λ = -2 be:
![m = \left[\begin{array}{ccc}2&1\\-2&-1\\\end{array}\right] \left[\begin{array}{c}m_1\\m_2\\\end{array}\right] = \left[\begin{array}{c}0\\0\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/vee8fauomn6bnhuu4bngj7dxzv89vo9drc.png)
![\sim v = \left[\begin{array}{ccc}2&1\\0&0\\\end{array}\right] \left[\begin{array}{c}m_1\\m_2\\\end{array}\right] = \left[\begin{array}{c}0\\0\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/5rivbhuo9neud7szelaf6m42pfaxshypsq.png)
Let m₂ = 1, m₁ = -1/2
![m = \left[\begin{array}{c}-1/2 \\1\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/5xmimfb0gz8txv6jnjnramjbrxc0nroj2b.png)
∴
![\left[\begin{array}{c}y_1\\y_2\\\end{array}\right]= C_1 e^(-t) \left[\begin{array}{c}-1\\1\\\end{array}\right] + C_2e^(-2t) \left[\begin{array}{c}-1/2\\1\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/vtaskmarhzcccs00gg80qfi79ordtdb7k6.png)
So as t → ∞
![\mathbf{ \left[\begin{array}{c}y_1\\y_2\\\end{array}\right]= \left[\begin{array}{c}0\\0\\\end{array}\right] \ \ so \ stable \ at \ node \ \infty }](https://img.qammunity.org/2021/formulas/mathematics/college/bncoes7zg81tameiplckpvlxvusgmuhufw.png)