Question

Let y 00 + by0 + 2y = 0 be the equation of a damped vibrating spring with mass m = 1, damping coefficient b > 0, and spring constant k = 2. (a) Convert this second order equation into a system of two first order equations. (b) Express the eigenvalues for this system in terms of b. (c) Describe the stability of the equilibrium solution ~0 for b > 2 √ 2. Justify your claim with information about the eigenvalues of the matrix for the system. (d) Connect the behavior of solutions near an equilibrium of this type with the spring mass system with damping coefficient b > 2 √ 2 and explain why your answer for part (c) is (or is not) what one should expect.

Answer 1

Explanation:

Given that:

The equation of the damped vibrating spring is y" + by' +2y = 0

(a) To convert this 2nd order equation to a system of two first-order equations;

let y₁ = y

y'₁ = y' = y₂

So;

y'₂ = y"₁ = -2y₁ -by₂

Thus; the system of the two first-order equation is:

y₁' = y₂

y₂' = -2y₁ - by₂

(b)

The eigenvalue of the system in terms of b is:

`\left|\begin{array}{cc}- \lambda &1&-2\ & -b- \lambda \end{array}\right|=0`

`-\lambda(-b - \lambda) + 2 = 0 \ \\ \\\lambda^2 +\lambda b + 2 = 0`

`\lambda = (-b \pm √(b^2 - 8))/(2)`

`\lambda_1 = (-b + √(b^2 -8))/(2) ; \ \lambda _2 = (-b - √(b^2 -8))/(2)`

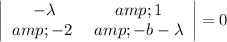
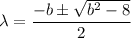
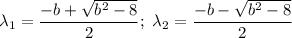
(c)

Suppose
`b > 2√(2)`, then λ₂ < 0 and λ₁ < 0. Thus, the node is stable at equilibrium.

(d)

From λ² + λb + 2 = 0

If b = 3; we get

`\lambda^2 + 3\lambda + 2 = 0 \\ \\ (\lambda + 1) ( \lambda + 2 ) = 0\\ \\ \lambda = -1 \ or \ \lambda = -2 \\ \\`

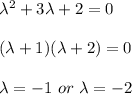
Now, the eigenvector relating to λ = -1 be:

`v = \left[\begin{array}{ccc}+1&1\\-2&-2\\\end{array}\right] \left[\begin{array}{c}v_1\\v_2\\\end{array}\right] = \left[\begin{array}{c}0\\0\\\end{array}\right]`

`\sim v = \left[\begin{array}{ccc}1&1\\0&0\\\end{array}\right] \left[\begin{array}{c}v_1\\v_2\\\end{array}\right] = \left[\begin{array}{c}0\\0\\\end{array}\right]`

Let v₂ = 1, v₁ = -1

`v = \left[\begin{array}{c}-1\\1\\\end{array}\right]`

Let Eigenvector relating to λ = -2 be:

`m = \left[\begin{array}{ccc}2&1\\-2&-1\\\end{array}\right] \left[\begin{array}{c}m_1\\m_2\\\end{array}\right] = \left[\begin{array}{c}0\\0\\\end{array}\right]`

`\sim v = \left[\begin{array}{ccc}2&1\\0&0\\\end{array}\right] \left[\begin{array}{c}m_1\\m_2\\\end{array}\right] = \left[\begin{array}{c}0\\0\\\end{array}\right]`

Let m₂ = 1, m₁ = -1/2

`m = \left[\begin{array}{c}-1/2 \\1\\\end{array}\right]`

∴

`\left[\begin{array}{c}y_1\\y_2\\\end{array}\right]= C_1 e^(-t) \left[\begin{array}{c}-1\\1\\\end{array}\right] + C_2e^(-2t) \left[\begin{array}{c}-1/2\\1\\\end{array}\right]`

So as t → ∞

`\mathbf{ \left[\begin{array}{c}y_1\\y_2\\\end{array}\right]= \left[\begin{array}{c}0\\0\\\end{array}\right] \ \ so \ stable \ at \ node \ \infty }`