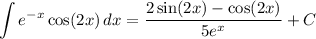Question

Integrate the following problem:


`\int {e^(-x) \cdot cos(2x)} \, dx`

P.S:
Have fun Lauren (and possibly Kelvy)!

Answer 1

`\displaystyle (2 \cdot sin2x-cos2x)/(5e^x) + C`

Explanation:

The integration by parts formula is:
`\displaystyle \int udv = uv - \int vdu`

Let's find u, du, dv, and v for
`\displaystyle \int e^-^x \cdot cos2x \ dx` .

• 
  `u=e^-^x`
• 
  `du=-e^-^x dx`

• 
  `dv=cos2x \ dx`
• 
  `v= (sin2x)/(2)`

Plug these values into the IBP formula:

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = e^-^x \cdot (sin2x)/(2) - \int (sin2x)/(2) \cdot -e^-^x dx`
• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = (e^-^x sin2x)/(2) - \int (sin2x)/(2) \cdot -e^-^x dx`

Now let's evaluate the integral
`\displaystyle \int (sin2x)/(2) \cdot -e^-^x dx`.

Let's find u, du, dv, and v for this integral:

• 
  `u=-e^-^x`
• 
  `du=e^-^x dx`
• 
  `dv=(sin2x)/(2) dx`
• 
  `v=(-cos2x)/(4)`

Plug these values into the IBP formula:

• 
  `\displaystyle \int -e^-^x \cdot (sin2x)/(x)dx = -e^-^x \cdot (-cos2x)/(4) - \int (-cos2x)/(4)\cdot e^-^x dx`

Factor 1/4 out of the integral and we are left with the exact same integral from the question.

• 
  `\displaystyle \int -e^-^x \cdot (sin2x)/(x)dx = -e^-^x \cdot (-cos2x)/(4) + (1)/(4) \int cos2x \cdot e^-^x dx`

Let's substitute this back into the first IBP equation.

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = (e^-^x sin2x)/(2) - \Big [ -e^-^x \cdot (-cos2x)/(4) + (1)/(4) \int cos2x \cdot e^-^x dx \Big ]`

Simplify inside the brackets.

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = (e^-^x sin2x)/(2) - \Big [ (e^-^x \cdot cos2x)/(4) + (1)/(4) \int cos2x \cdot e^-^x dx \Big ]`

Distribute the negative sign into the parentheses.

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = (e^-^x sin2x)/(2) - (e^-^x \cdot cos2x)/(4) - (1)/(4) \int cos2x \cdot e^-^x dx`

Add the like term to the left side.

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx + (1)/(4) \int cos2x \cdot e^-^x dx= (e^-^x sin2x)/(2) - (e^-^x \cdot cos2x)/(4)`
• 
  `\displaystyle (5)/(4) \int e^-^x \cdot cos2x \ dx = (e^-^x sin2x)/(2) - (e^-^x \cdot cos2x)/(4)`

Make the fractions have common denominators.

• 
  `\displaystyle (5)/(4) \int e^-^x \cdot cos2x \ dx = (2e^-^x sin2x)/(4) - (e^-^x \cdot cos2x)/(4)`

Simplify this equation.

• 
  `\displaystyle (5)/(4) \int e^-^x \cdot cos2x \ dx = (2e^-^x sin2x - e^-^x cos2x)/(4)`

Multiply the right side by the reciprocal of 5/4.

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = (2e^-^x sin2x - e^-^x cos2x)/(4) \cdot (4)/(5)`

The 4's cancel out and we are left with:

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = (2e^-^x sin2x - e^-^x cos2x)/(5)`

Factor
`e^-^x` out of the numerator.

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = (e^-^x(2 \cdot sin2x-cos2x))/(5)`

Simplify this by using exponential properties.

• 
  `\displaystyle \int e^-^x \cdot cos2x \ dx = (2 \cdot sin2x-cos2x)/(5e^x)`

The final answer is
`\displaystyle \int e^-^x \cdot cos2x \ dx = (2 \cdot sin2x-cos2x)/(5e^x) + C`.

Answer 2

`\displaystyle\int e^(-x)\cos(2x)\, dx=(2\sin(2x)-\cos(2x))/(5e^x)+C`

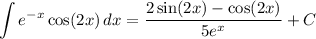
Explanation:

We would like to integrate the following integral:

`\displaystyle \int e^(-x)\cdot \cos(2x)\, dx`

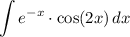
Since this is a product of two functions, we can consider using Integration by Parts given by:

`\displaystyle \int u\, dv =uv-\int v\, du`

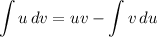
So, let’s choose our u and dv. We can choose u base on the following guidelines: LIATE; or, logarithmic, inverse trig., algebraic, trigonometric, and exponential.

Since trigonometric comes before exponential, we will let:

`u=\cos(2x)\text{ and } dv=e^(-x)\, dx`

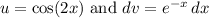
By finding the differential of the left and integrating the right, we acquire:

`du=-2\sin(2x)\text{ and } v=-e^(-x)`

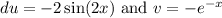
So, our integral becomes:

`\displaystyle \int e^(-x)\cdot \cos(2x)\, dx=(\cos(2x))(-e^(-x))-\int (-e^(-x))(-2\sin(2x))\, dx`

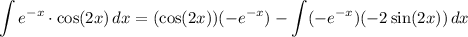
Simplify:

`\displaystyle \int e^(-x)\cdot \cos(2x)\, dx=-e^(-x)\cos(2x)-2\int e^(-x)\sin(2x)\, dx`

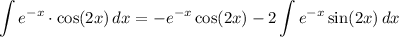
Since we ended up with another integral of a product of two functions, we can apply integration by parts again. Using the above guidelines, we get that:

`u=\sin(2x)\text{ and } dv=e^(-x)\, dx`

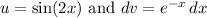
By finding the differential of the left and integrating the right, we acquire:

`du=2\cos(2x)\, dx\text{ and } v=-e^(-x)`

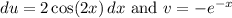
This yields:

`\displaystyle \int e^(-x)\cdot \cos(2x)\, dx=-e^(-x)\cos(2x)-2\Big[(\sin(2x))(-e^(-x))-\int (-e^(-x))(2\sin(2x))\, dx\Big]`

Simplify:

`\displaystyle \int e^(-x)\cdot \cos(2x)\, dx=-e^(-x)\cos(2x)-2\Big[-e^(-x)\sin(2x)+2\int e^(-x)\cos(2x)\, dx\Big]`

We can distribute:

`\displaystyle \int e^(-x)\cdot \cos(2x)\, dx=-e^(-x)\cos(2x)+2e^(-x)\sin(2x)-4\int e^(-x)\cos(2x)\, dx`

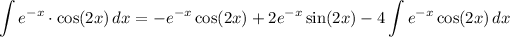
The integral on the right is the same as our original integral. So, we can isolate it:

`\displaystyle \Big(\int e^(-x)\cos(2x)\, dx\Big)+4\Big(\int e^(-x)\cos(2x)\, dx)\Big)=-e^(-x)\cos(2x)+2e^(-x)\sin(2x)`

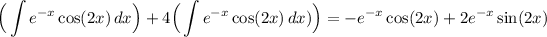
Combine like integrals:

`\displaystyle 5 \int e^(-x)\cos(2x)\, dx=-e^(-x)\cos(2x)+2e^(-x)\sin(2x)`

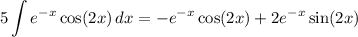
We can factor out an e⁻ˣ from the right:

`\displaystyle 5\int e^(-x)\cos(2x)\, dx=e^(-x)\Big(-\cos(2x)+2\sin(2x)\Big)`

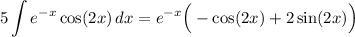
Dividing both sides by 5 yields:

`\displaystyle \int e^(-x)\cos(2x)\, dx=(e^(-x))/(5)\Big(-\cos(2x)+2\sin(2x)\Big)`

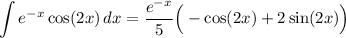
Rewrite. We of course also need the constant of integration. Therefore, our final answer is:

`\displaystyle\int e^(-x)\cos(2x)\, dx=(2\sin(2x)-\cos(2x))/(5e^x)+C`