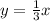Question

What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment?

y = One-thirdx
y = One-thirdx – 2
y = 3x
y = 3x − 8

Answer 1

A. y = One-thirdx

Explanation:

2020 Edge

Answer 2

Complete Question:

The given line segment has a midpoint at (3, 1). On a coordinate plane, a line goes through (2, 4), (3, 1), and (4, -2).

What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment?

Answer:

`y = (1)/(3)x`

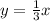
Explanation:

From the question, we understand that the line goes through
`(2, 4), (3, 1), and\ (4, -2).`

First, we calculate the slope of the above points

`m = (y_2 - y_1)/(x_2 - x_1)`

Where

`(x_1,y_1) = (2,4)`

`(x_2,y_2) = (3,1)`

`m = (1 - 4)/(3 - 2)`

`m = (-3)/(1)`

`m = -3`

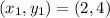
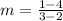
Also; from the question, we understand that the line segment is perpendicular to the above points.

This slope (m2) of the line segment is calculated as:

`m_2 = -(1)/(m)`

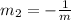
Substitute -3 for m

`m_2 = -(1)/(-3)`

`m_2 = (1)/(3)`

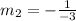
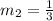
Lastly, we calculate the equation of the line using:

`y - y_1 = m_2(x - x_1)`

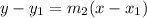
The line segment has a midpoint at (3, 1)

So:

`y - 1 = (1)/(3)(x - 3)`

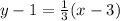
Open bracket

`y - 1 = (1)/(3)x - 1`

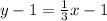
Add 1 to both sides

`y - 1 +1= (1)/(3)x - 1+1`

`y = (1)/(3)x`

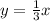
Hence, the equation of the line segment is:
`y = (1)/(3)x`