The exact value of
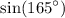 is
is
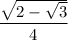 , which is option C.
, which is option C.
The exact value of
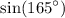 is
is
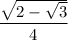 . This corresponds to option C.
. This corresponds to option C.
To find this value, we can use the angle addition formula for sine:
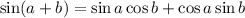
In this case, we can rewrite
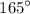 as the sum of
as the sum of
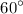 and
and
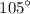 . So, we have:
. So, we have:

Now, let's use the values of sine and cosine for
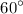 and
and
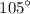 :
:
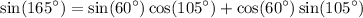
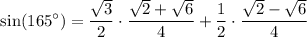
Simplifying this expression, we get:
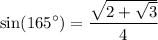
Therefore, option C is the correct answer.