Answer:
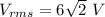
Step-by-step explanation:
Given that,
The maximum voltage of an alternating current,
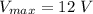
We need to find the highest Vrms that can be supplied to this component while staying below the voltage limit.
Let rms voltage in terms of peak voltage is given by :
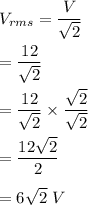
Hence, the required rms voltage is
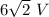 .
.