The sampling distribution of the difference in the proportions between proportion is given by possible values of the difference.
The mean of the difference in sample proportion is; (E) 0.22 - 0.36
Reasons:
The given information are;
Percentage of eastern gray squirrel population weighing over 0.5 kg = 22%
Percentage of western gray squirrel population weighing over 0.5 kg = 36%
Sample size of the eastern gray squirrels = 60
Sample size of the western gray squirrels = 120
Required:
The mean of the sampling distribution of the difference in sample proportions (eastern minus western)
The mean of the difference is given by the difference of the mean.
The mean of the sampling distribution of the difference in the sampling proportion from two populations is; Mean = p₁ - p₂
Where;
p₁ = The proportion of the eastern gray squirrel = 22% = 0.22
p₂ = The proportion of the western gray squirrel = 36% = 0.36
Therefore;
Mean = p₁ - p₂ = 0.22 - 0.36
The correct option is (E) 0.22 - 0.36
Learn more here:
The possible question options obtained online includes;
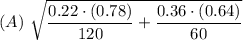
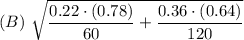
(C) 60·(0.22) - 120·(0.36)
(D) 0.36 - 0.22
(E) 0.22 - 0.36