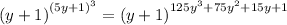Note: Your expression sounds a little unclear, so I am assuming your expression is
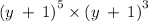
But, the procedure to solve the expressions involving exponents remains the same, so whatever the expression is, you may be able to get your concept clear.
In the end, I will solve both expressions.
Answer:
Please check the explanation
Explanation:
Given the expression
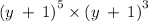
solving the expression
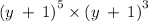
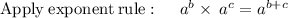
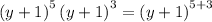
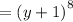
Therefore, we conclude that:

IF YOUR EXPRESSION IS THIS
↓
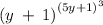
solving the expression
as
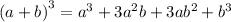
so

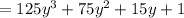
Thus, the expression becomes