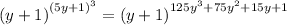Question

Simplify (y + 1)^5y + 1)^3​

Answer 1

Note: Your expression sounds a little unclear, so I am assuming your expression is

`\left(y\:+\:1\right)^5* \left(y\:+\:1\right)^3`

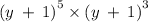
But, the procedure to solve the expressions involving exponents remains the same, so whatever the expression is, you may be able to get your concept clear.

In the end, I will solve both expressions.

Answer:

Please check the explanation

Explanation:

Given the expression

`\left(y\:+\:1\right)^5* \left(y\:+\:1\right)^3`

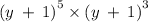
solving the expression

`\left(y\:+\:1\right)^5* \left(y\:+\:1\right)^3`

`\mathrm{Apply\:exponent\:rule}:\quad \:a^b* \:a^c=a^(b+c)`

`\left(y+1\right)^5\left(y+1\right)^3=\left(y+1\right)^(5+3)`

`=\left(y+1\right)^8`

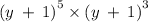
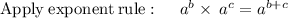
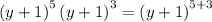
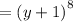
Therefore, we conclude that:

`\left(y\:+\:1\right)^5* \left(y\:+\:1\right)^3=\left(y+1\right)^8`

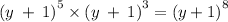
IF YOUR EXPRESSION IS THIS

↓

`\left(y\:+\:1\right)^(\left(5y+1\right)^3)`

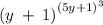
solving the expression

as

`\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3`

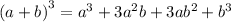
so

`\left(5y+1\right)^3=125y^3+75y^2+15y+1`

`=125y^3+75y^2+15y+1`

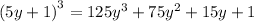
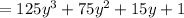
Thus, the expression becomes

`\left(y+1\right)^(\left(5y+1\right)^3)=\left(y+1\right)^(125y^3+75y^2+15y+1)`