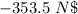Question

The vertical force f acts downward at A on the two membered frames. Determine the magnitude of the two components of F directed along axes of AB and AC. Set F=500N

Answer 1

The magnitude will be "353.5 N". A further solution is given below.

Step-by-step explanation:

The given values is:

F = 500 N

According to the question,

In ΔABC,

⇒
`\angle BCA = (90-30)`

⇒
`=60^(\circ)`

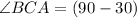
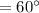
then,

⇒
`\angle BAC=(180-45-60)`

⇒
`=75^(\circ)`

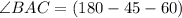
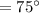
Now,

The corresponding angle will be:

⇒
`\angle FAC=60^(\circ)`

⇒
`\angle FAB=70+60`

⇒
`=135^(\circ)`

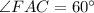
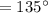
Aspect of F across the AC arm will be:

=
`F* cos(60)`

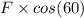
On putting the values of F, we get

=
`500* (.5)`

=
`200 \ Newton`

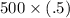
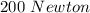
Component F along the AC (in magnitude) will be:

=
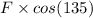
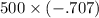
`F* cos(135)`

=
`500* (-.707)`

=
`-353.5 \ N \`