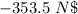Answer:
The magnitude will be "353.5 N". A further solution is given below.
Step-by-step explanation:
The given values is:
F = 500 N
According to the question,
In ΔABC,
⇒
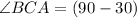
⇒
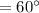
then,
⇒
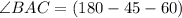
⇒
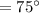
Now,
The corresponding angle will be:
⇒
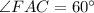
⇒

⇒
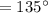
Aspect of F across the AC arm will be:
=
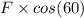
On putting the values of F, we get
=
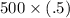
=
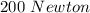
Component F along the AC (in magnitude) will be:
=
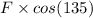
=
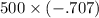
=