Question

Ideal gas helium flows through the inlet of an isentropic nozzle with a velocity of 25 m/s, and the exit flow is at 100 kPa, 300 K, and has a velocity of 250 m/s. a. Determine the inlet temperature. b. Determine the inlet pressure. c. Determine the area ratio between inlet and exit

Answer 1

a. The inlet temperature is approximately 305.232 K

b. The inlet pressure is approximately 452.0108 kPa

c. The area ratio between the inlet and exit is approximately 2.2509

Step-by-step explanation:

a. From the energy equation related to the question, we have;

`C_p \cdot (T_i - T_e) = (1)/(2) \cdot \left (v_e^2 - v_1^2 \right)`

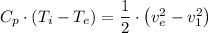
Where;

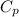`C_p` = The specific heat capacity for helium = 5.913 kJ/(kg·K)

`T_i` = The inlet temperature

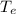`T_e` = The exit temperature = 300 K

`v_i` = The inlet velocity = 25 m/s

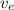`v_e` = The exit velocity = 250 m/s

Therefore, we have;

`T_i= ( (1)/(2) \cdot \left (v_e^2 - v_1^2 \right))/(C_p) + T_e = ( (1)/(2) * \left (250^2 - 25^2 \right))/(5.913 * 1000) + 300 \approx 305.232`

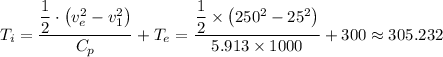
The inlet temperature =
`T_i` ≈ 305.232 K

b. From the following equation for the critical pressure, for helium, we have;

`(P_c)/(P_i) = \left ((2)/(n + 1) \right ) ^{(n)/(n - 1) } = 0.487`

Where;

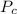`P_c` = The critical pressure = 2.26 atm for helim

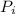`P_i` = The inlet pressure

n = The polytropic constant

We have;

`(2.26 \ atm)/(P_i) = 0.487`

`\therefore P_i = (2.26 \ atm)/(0.487) \approx 4.641 \ atm`

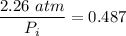
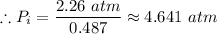
The inlet pressure,
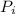`P_i` ≈ 4.641 atm ≈ 452.0108 kPa

c. The inlet to exit pressure ratio is given as follows;

`P_e = (A_i * T_e * v_i)/(A_e * T_i * v_e) * P_i`

Therefore, we have;

`(A_i)/(A_e) = (P_e * T_i * v_e)/( T_e * v_i * P_i) = (100 * 305.232 * 250)/( 300 * 25 * 452.0108) = 2.2509`

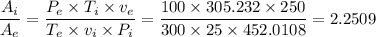
The area ratio between the inlet and exit,
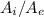`A_i/A_e` ≈ 2.2509.