Question

12) Find the sum, S7 for the geometric series {1 + 5 + 25 + - + 15625).

[A] S, = 19531
[B] S, = 16536
[C] Sy = 15631
D] S, = 31256
[E] None of these

Answer 1

Understanding:

The sum of a geometric series is,
`a+ar+ar^2+ar^3+...`, with a being the start point and r is the common ratio. We can also use the following formula to make life easier
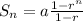`S_n=a(1-r^n)/(1-r)`, a is your start point, r is the common ratio, and n is the number of terms, which in our case is S7.

Solution:

Our start point is 1,
`a=1`,

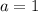The common ratio is 5,
`r=5`,

And finally, the number of terms is 7,
`n=7`.

`S_n=a(1-r^n)/(1-r) \\=(1)(1-(5)^((7)))/(1-(5)) \\=(1-78125)/(1-5) \\=(-78124)/(-4)\\=19531`

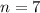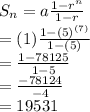
The answer is [A] 19531.