Answer:
the probability that more than 9 but fewer than 14 disapprove of smoking pot daily is 0.608
Explanation:
From the information given:
Let N represent the total number of senior students
N = 17000
and k to be the number of seniors disapproving of daily pot smoking
k = 17000 × 0.70
k = 11900
sample size n = 18
Suppose X represents the random variable...
Then,
X = 0,1,2,...,18
Thus X follows a hypergeometric distribution with parameters
(N = 17000, n = 18 & k = 11900)
Thus, the probability mass function is:
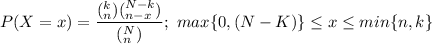
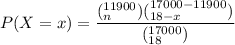

Now, the required probability is computed as:

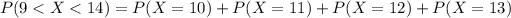
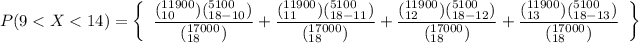 P(9<X<14) = 0.0811 + 0.1377 + 0.1874 + 0.2018
P(9<X<14) = 0.0811 + 0.1377 + 0.1874 + 0.2018
P(9<X<14) = 0.608
Thus, the probability that more than 9 but fewer than 14 disapprove of smoking pot daily is 0.608