Question

g A nationwide survey of 17,000 college seniors by the University of Michigan revealed that almost 70% disapprove of daily pot smoking. If 18 of these seniors are selected at random and asked their opinion, what is the probability that more than 9 but fewer than 14 disapprove of smoking pot daily

Answer 1

the probability that more than 9 but fewer than 14 disapprove of smoking pot daily is 0.608

Explanation:

From the information given:

Let N represent the total number of senior students

N = 17000

and k to be the number of seniors disapproving of daily pot smoking

k = 17000 × 0.70

k = 11900

sample size n = 18

Suppose X represents the random variable...

Then,

X = 0,1,2,...,18

Thus X follows a hypergeometric distribution with parameters

(N = 17000, n = 18 & k = 11900)

Thus, the probability mass function is:

`P(X =x) = ((^k_n) (^(N-k)_(n-x) ) )/((^N_n) ); \ max \{0,(N-K) \} \le x \le min \{n,k\}`

`P(X =x) = ((^(11900)_n) (^(17000-11900)_(18-x) ) )/((^(17000)_(18)) )`

`P(X =x) = ((^(11900)_n) (^(51000)_(18-x) ) )/((^(17000)_(18)) ); \ 0\le x \le 18`

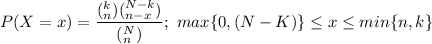
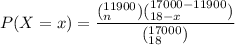
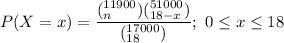
Now, the required probability is computed as:

`P(9<X<14) = P(10 \le X \le13)`

`P(9<X<14) = P(X =10) +P(X =11) +P(X=12) +P(X =13)`

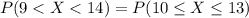
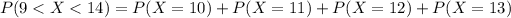
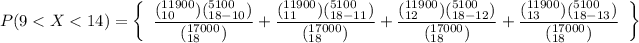`P(9<X<14) = \left\{\begin{array}{c} ((^(11900)_(10)) (^(5100)_(18-10)) )/((^(17000)_(18))) + ((^(11900)_(11)) (^(5100)_(18-11)) )/((^(17000)_(18)))+ ((^(11900)_(12)) (^(5100)_(18-12)) )/((^(17000)_(18))) + ((^(11900)_(13)) (^(5100)_(18-13)) )/((^(17000)_(18)))\end{array}\right\}`P(9<X<14) = 0.0811 + 0.1377 + 0.1874 + 0.2018

P(9<X<14) = 0.608

Thus, the probability that more than 9 but fewer than 14 disapprove of smoking pot daily is 0.608