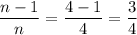Let the original fraction be
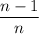
Now let's increase both numerator and denominator by 2:
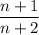
This produces a 1/12 increase:
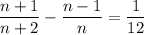
The left hand side can be rearranged as
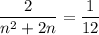
Invert both sides:

Solve the quadratic equation:
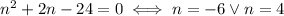
So, in the first case, the original fraction is
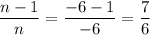
In the second case, we have