Question

If sinB = 3/5, find the value of tanB *​

Answer 1

`\boxed {\boxed {\sf tan (B)=3/4}}`

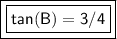
Explanation:

First, recall the right triangle trigonometry ratios.

• sin(θ)= opposite/hypotenuse
• cos(θ)= adjacent/hypotenuse
• tan (θ)= opposite/adjacent

We are looking for tangent, so we will use the last ratio.

We know that the sine of B is 3/5. Since sine is opposite over hypotenuse, the opposite is 3 and the hypotenuse is 5.

But, tangent needs opposite and adjacent.

We have to find the adjacent. This can be done using the Pythagorean Theorem, because these ratios are used with right triangles.

`a^2+b^2=c^2`

where a and b are the legs and c is the hypotenuse.

We know the hypotenuse is 5 and one of the legs is 3.

`(3)^2+b^2=(5)^2`

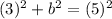
Solve the exponents.

• (3)²= 3*3=9
• (5)²=5*5=25

`9+b^2=25`

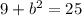
Subtract 9 from both sides of the equation to isolate the variable.

`9-9+b^2=25-9\\b^2=25-9\\b^2=16`

b is being squared. The inverse of a square is the square root. Take the square root of both sides.

`√(b^2)=√(16) \\b=√(16) \\b=4`

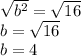
The adjacent side is 4.

Now we know the opposite (3) and adjacent (4). We can substitute these into the tangent ratio.

tan(θ)= opposite/adjacent

tan(B)=3/4

The tangent of B is 3/4