Answer:
40 square units
Explanation:
The question gives that both the large shape and the small missing shape are rectangles. The formula for the area of a rectangle is
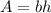 where "A" is the "Area", "b" is the "base" (bottom edge), and "h" is the height (side edge).
where "A" is the "Area", "b" is the "base" (bottom edge), and "h" is the height (side edge).
For rectangles, opposite sides (example: top & bottom) have the same length, so the top of the missing rectangle must also be 3.
To find the area of the figure, we must find the difference (subtraction) between the large rectangle (without a hole out of it) and the rectangular hole.
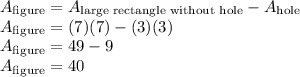
So, the area of the figure is 40 square units.