Answer:
The perimeter of the square LAMP is 8
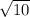 units
units
Explanation:
The rule of the distance between two points (x1, y1) and (x2, y2) is
d =
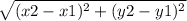
∵ LAMP is a square
∵ The sides of the square are equal in lengths
∴ LA = AM = MP = PL
Let us find the length of one side of it
∵ L = (-2, -3) and A = (4, -1)
∴ x1 = -2 and y1 = -3
∴ x2 = 4 and y2 = -1
→ Substitute them in the rule of the distance above to find LA
∵ LA =

∴ LA =
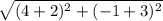
∴ LA =
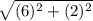
∴ LA =
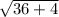 =
=
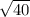
→ Simplify the root
∴ LA = 2
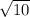 units
units
∵ The perimeter of the square = 4 × side
∴ The perimeter of the square = 4 × 2
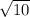
∴ The perimeter of the square = 8
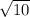
∴ The perimeter of the square LAMP is 8
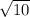 units
units