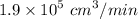Solution :
The diameter of the tank = 3 m = 300 cm
Radius of the tank = 1.5 m = 150 cm
Height of the tank = 8 m = 800 cm
The rate of increase of height of water level = 26 cm/min
∴
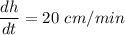
The water is leaking at a rate of = 10700 cubic centimeters per min
∴ rate out = 10,700
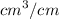
At time 't', the height of water level is 'h' with radius 'r' and volume 'V'.
By the property of similarity of triangles we can write
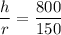
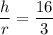
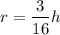
Volume of water at time 't' is given as
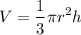
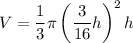
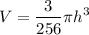
Now differentiating w.r.t 't'
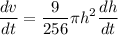
The rate of increase in tank = rate of inward flow - rate of outward flow
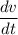 = rate of inward flow - 10,700
= rate of inward flow - 10,700
rate of inflow = 10,700 +
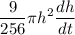
Substituting the values we get
rate of inflow = 10,700 +
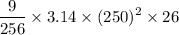
∴ rate of inward flow =