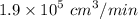Question

Water is leaking out of an inverted conical tank at a rate of 10700 cubic centimeters per min at the same time that water is being pumped into the tank at a constant rate. The tank has height 8 meters and the diameter at the top is 3 meters. If the water level is rising at a rate of 26 centimeters per minute when the height of the water is 2.5 meters, find the rate at which water is being pumped into the tank in cubic centimeters per minute.

Answer 1

The diameter of the tank = 3 m = 300 cm

Radius of the tank = 1.5 m = 150 cm

Height of the tank = 8 m = 800 cm

The rate of increase of height of water level = 26 cm/min

∴
`$(dh)/(dt) = 20 \ cm/min$`

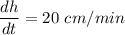
The water is leaking at a rate of = 10700 cubic centimeters per min

∴ rate out = 10,700
`$cm^3 / cm $`

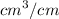
At time 't', the height of water level is 'h' with radius 'r' and volume 'V'.

By the property of similarity of triangles we can write

`$(h)/(r) = (800)/(150) $`

`$(h)/(r) = (16)/(3) $`

`$r = (3)/(16)h$`

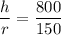
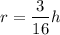
Volume of water at time 't' is given as

`$V= (1)/(3) \pi r^2 h $`

`$V= (1)/(3) \pi \left((3)/(16)h\right)^2 h $`

`$V =(3)/(256) \pi h^3$`

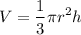
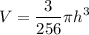
Now differentiating w.r.t 't'

`$(dv)/(dt) = (9)/(256) \pi h^2 (dh)/(dt)$`

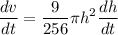
The rate of increase in tank = rate of inward flow - rate of outward flow

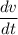`$(dv)/(dt) $` = rate of inward flow - 10,700

rate of inflow = 10,700 +
`$ (9)/(256) \pi h^2 (dh)/(dt)$`

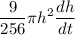
Substituting the values we get

rate of inflow = 10,700 +
`$ (9)/(256) * 3.14 * (250)^2 * 26$`

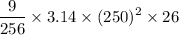
∴ rate of inward flow =
`$1.9 * 10^5 \ cm^3/min$`