Question

Suppose we wish to demonstrate that there is a difference between the proportions of wives and husbands who do laundry at home. From a random sample of 66 randomly selected wives, we observe 44 who do laundry at home. From a random sample of 46 husbands, we observe 18 who do laundry at home. Test the claim that the proportion of wives, p 1 , who do laundry at home is different from the proportion of husbands, p 2 , who do laundry at home. Use a 1% significance level.

Answer 1

Explanation:

From this study:

The null hypothesis:

`H_o : p_1 =p_2`

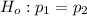
The altenative is:

`H_a : p_1 \\e p_2`

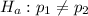
This test is a two-tailed test.

However; we are told that the wives have 44 success out of 66, then the number of failures will be 22.

Then;

`\hat p_1 = (44)/(66)`

`\hat p_1 = 0.6667`

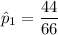
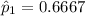
Similarly, the husbands have 18 success out of 46, then the number of failures will be 28

Then:

`\hat p_2 = (18)/(46)`

`\hat p_2 = 0.3913`

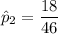
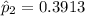
The pooled proportion
`p = (18+44)/(66+46)`

`p = (62)/(112)`

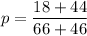
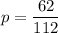
p = 0.55357

The estimated standard error S.E is:

`= \sqrt{( \bar p(1- \bar p))/(n_1) +( \bar p(1-\bar p))/(n_2)}`

=
`\sqrt{ 0.55357(1-0.55357) \Big( (1)/(66) + (1)/(46) \Big)}`

`=√( 0.55357(0.44643) \Big(0.01515 + 0.021739 \Big))`

`=√( 0.00911638798)`

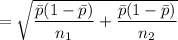
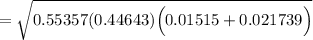
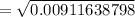
= 0.0955

The Z test statitics can now be computed as:

`Z = \frac{ \hat p_1 - \hat p_2}{\sqrt{( \bar p(1- \bar p))/(n_1) +( \bar p(1-\bar p))/(n_2)}}`

`Z = (0.6667 -0.3913)/(0.0955)`

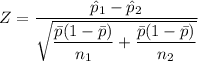
Z = 2.88

Th p -value from the test statistics is:

p-value = 2P(Z > 2.88)

p- value = 2 P (1 - Z < 2.88)

p-value = 2 ( 1 - 0.998)

p-value = 2 ( 0.002)

p -alue = 0.004

Decision Rule:

Thus, at 0.01 significance level, we reject the null hypothesis because, p-value is less than that (i.e. significance level)

Conclusion:

We conclude that there is a significant difference between the proportions.