Two sides of a triangle are two consecutive number, whose area is 17.5cm². Find the numbers

Question

asked Aug 5, 2021 199k views

1 Answer

Rashed Hasan · Answer 1 · 2021-08-10T13:54:57+0000

Answer:

The numbers associated with the triangle are 5.437 and 6.437 centimeters, respectively.

Explanation:

Two numbers are consecutives, when their difference is equal to 1. The area of the triangle is determined by the following formula:

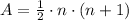
$A = (1)/(2)\cdot n \cdot (n+1)$

$A = (1)/(2)\cdot (n^(2)+n)$

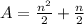
A = (n^(2))/(2)+(n)/(2)

$n^(2)+n = 2\cdot A$

Where
is the shortest length of the triangle, measured in centimeters.

And we get the following second-order polynomial:

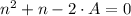$n^(2)+n -2\cdot A = 0$ (1)

If we know that
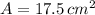$A = 17.5\,cm^(2)$ , then the shortest length of the triangle is:

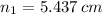$n_(1) = 5.437\,cm$ and
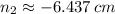
$n_(2) \approx -6.437\,cm$

Since length is a positive variable, the only possible solution is:

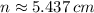
$n\approx 5.437\,cm$

Then, the numbers associated with the triangle are 5.437 and 6.437 centimeters, respectively.