Question

Is this a square root graph?

Is this graph a reflection of its parent graph?
this graph shifted _
The equation to this graph would transform the parent function f(x) to _

Answer 1

Thus,
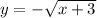`y=-√(x+3)` represents the transformed graph on the attached figure, which is a translated square root graph i.e. vertically reflected across the y-axis and also horizontally translated or shifted 3 units to the left.

Explanation:

Consider the function

y = f(x)

The rule of horizontal translation

y = f(x-h)

When 'h' is positive, the function is shifted to the right.

When 'h' is negative, the function is shifted to the left.

The rule of implying vertical reflection across the x-axis

y = -f(x)

Applying the rule:

We know that the square root function is

`y=√(x)`

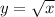
We know that if the graph would be reflected across the x-axis, then

`y=-√(x)`

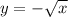
We know that is horizontally translated or shifted 3 units to the left, it implies +

3 inside the radical implies. Then the transformed function becomes .

Please check the attached diagram. From the diagram,

• The blue graph shows the parent function
  `y=√(x)`.

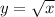• The red graph shows the transformed function i.e. vertically reflected across the y-axis and also horizontally translated or shifted 3 units to the left.

Thus,
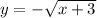`y=-√(x+3)` represents the transformed graph on the attached figure, which is a translated square root graph i.e. vertically reflected across the y-axis and also horizontally translated or shifted 3 units to the left.