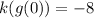Question

Show your work F(x)=5x^2-4x+1 G(x)=3x-2 H(x)=x+1 K(x)= 4x What is (g*h)(x)= What is g(k(x))= What is k(g(0)) =

Answer 1

— What is (g × h)(x)?

The answer is 3x²+x-2

— What is g(k(x))?

The answer is 12x - 2 or 2(6x-1)

— What is k(g(0))

The answer is -8

Step-by-step explanation:

Given these functions —

`f(x) = 5 {x}^(2) - 4x + 1 \\ g(x) = 3x - 2 \\ h(x) = x + 1 \\ k(x) = 4x`

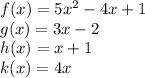
Find (g × h)(x)

`(g * h)(x) = g(x) * h(x)`

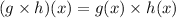
Substitute g(x) = 3x - 2 and h(x) = x + 1

`(3x - 2) * (x + 1) \\ (3x - 2)(x + 1)`

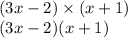
Multiply the polynomial.

`3 {x}^(2) + 3x - 2x - 2`

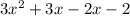
Subtract - 2x out of 3x —

`3 {x}^(2) + x - 2`

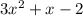
Thus, the answer is —

`(g * h)(x) = 3 {x}^(2) + x - 2`

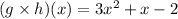
Find (g(k(x))

Substitute k(x) = 4x in g(x).

`g(x) = 3x - 2 \\ k(x) = 4x`

`g(k(x)) = g(4x)`

`g(4x) = 3(4x) - 2`

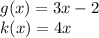
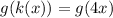
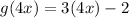
Distribute 3 in 4x —

`g(4x) = 12x - 2`

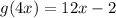
Thus the answer is —

`g(k(x)) = 12x - 2`

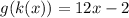
Alternative Solution

`g(k(x)) = 2(6x - 1)`

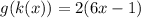
Find k(g(0))

Given two functions — k(x) and g(x)

`k(x) = 4x \\ g(x) = 3x - 2`

Evaluate the value of g(0) as we substitute x = 0 in g(x)

`g(0 ) = 3(0) - 2 \\ g(0) = 0 - 2 \\ g(0) = - 2`

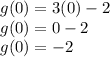
Since we need to find k(g(0)), our currently input is g(0).

From k(x) and g(0) —

`k(x) = 4x \\ g(0) = - 2`

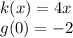
Substitute g(0) = -2 in k(x)

`k(g(0)) = 4(g(0)) \\ k( - 2) = 4( - 2) \\ k( - 2) = - 8`

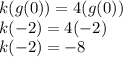
Thus, the answer is —

`k(g(0)) = - 8`