Question

A rigid, 28-L steam cooker is arranged with a pressure relief valve set to release vapor and maintain the pressure once the pressure inside the cooker reaches 150 kPa. Initially, this cooker is filled with water at 175 kPa with a quality of 10 percent. Heat is now added until the quality inside the cooker is 40 percent. The water is stirred at the same time that it is being heated. Determine the minimum entropy change of the heat-supplying source if 100 kJ of work is done on the water as it is being heated. Use steam tables.

Answer 1

`\Delta S_(source)>-1.204(kJ)/(K)`

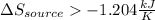
Step-by-step explanation:

Hello!

In this case, given the initial conditions, we first use the 10-% quality to compute the initial entropy:

`s_1=s_(f,175kPa)+q*s_(fg,175kPa)\\\\s_1=1.4850(kJ)/(kg*K) +0.1*5.6865(kJ)/(kg*K)=2.0537(kJ)/(kg*K)`

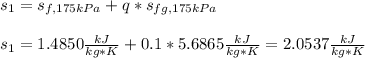
Now the entropy at the final state given the new 40-% quality:

`s_2=s_(f,150kPa)+q*s_(fg,150kPa)\\\\s_2=1.4337(kJ)/(kg*K) +0.4*5.7894(kJ)/(kg*K)=3.7495(kJ)/(kg*K)`

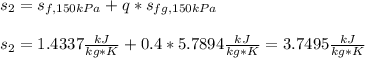
Next step is to compute the mass of steam given the specific volume of steam at 175 kPa and the 10% quality:

`m_1=(0.028m^3)/((0.001057+0.1*1.002643)(m^3)/(kg) ) =0.274kg\\\\m_2=(0.028m^3)/((0.001053+0.4*1.158347)(m^3)/(kg) ) =0.0603kg`

Then, we can write the entropy balance:

`\Delta S_(source)+(Q)/(T_1) -(Q)/(T_2) +s_2m_2-s_1m_1-s_(fg)(m_2-m_1)>0`

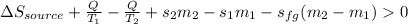
Whereas sfg stands for the entropy of the leaving steam to hold the pressure at 150 kPa and must be greater than 0; thus we plug in:

Which is such minimum entropy change of the heat-supplying source.

Best regards!