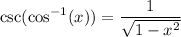Write the expression as an algebraic expression of x that does not involve trigonometric functions: csc({cos}^( - 1) x) ​

Question

Write the expression as an algebraic expression of x that does not involve trigonometric functions:


`csc({cos}^( - 1) x)`
​

Answer 1

`\displaystyle \csc(\cos^(-1)(x))=(1)/(√(1-x^2))`

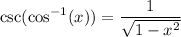
Explanation:

Please refer to the attachment.

We have:

`\csc(\cos^(-1)(x))`

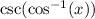
First, we will let:

`\cos^(-1)(x)=\theta`

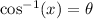
Then:

`x=\cos(\theta)`

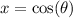
So, the adjacent side of our triangle is x and the hypotenuse is 1.

Then by the Pythagorean Theorem, the opposite side is given by:

`x^2+o^2=1^2`

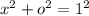
So:

`o=√(1-x^2)`

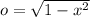
Going back, we have:

`\csc(\cos^(-1)(x))`

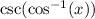
Since arccos(x) is θ:

`=\csc(\theta)`

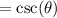
Cosecant is the ratio of the hypotenuse over the opposite side. Therefore:

`\displaystyle \csc(\theta)=(1)/(√(1-x^2))`

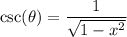
Hence:

`\displaystyle \csc(\cos^(-1)(x))=(1)/(√(1-x^2))`