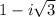Explanation:
x^3 is a perfect cube, 8 is a perfect cube, so we use difference of cubes.
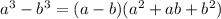
Cube root of x^3 is x.
Cube root of 8 is 2
So
a=x
b= 2.
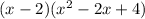
Set these equations equal to zero
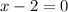
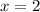
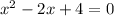
If we do the discriminant, we get a negative answer so we would have two imaginary solutions,
Thus the only real root is 2.
If you want imaginary solutions, apply the quadratic formula.
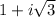
and