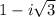3. What are the roots of the polynomial y = x³ - 8?

Question

asked Jan 3, 2023 143k views

1 Answer

Mihae Kheel · Answer 1 · 2023-01-10T20:00:59+0000

Explanation:

x^3 is a perfect cube, 8 is a perfect cube, so we use difference of cubes.

${a}^(3) - {b}^(3) = (a - b)( {a}^(2) + ab + {b}^(2) )$

Cube root of x^3 is x.

Cube root of 8 is 2

So

a=x

b= 2.

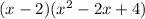
$(x - 2)( {x}^(2) - 2x + 4)$

Set these equations equal to zero

x - 2 = 0

x = 2

${x}^(2) - 2x + 4 = 0$

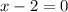
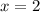
If we do the discriminant, we get a negative answer so we would have two imaginary solutions,

Thus the only real root is 2.

If you want imaginary solutions, apply the quadratic formula.

1 + i √( 3 )

and

1 - i √(3)