Question

Simplify. Use the distributive

property and combining like terms to
simplify each expression.
7. 5x + 2(x – 3),

Answer 1

Combining like terms is a process where you combine the terms with the same variable and/or exponent.

Let's say that we have an expression 3p + 3q. We can't combine the like terms, because 3p and 3q have different variables.

Now, what is the distributive property?

The distributive property is a property used for multiplying a monomial by a binomial or trinomial by "distributing" the monomial. The distributive property has a formula, which is:

`\sf{a(b+c)=ab+ac}`

Here, a got multiplied by b and c.

Similarly, we combine the terms:

`\sf{5x+2(x-3)}`

Simplify:

`\sf{5x+2x-6}`

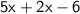
Combine like terms:

`\sf{7x-6}`

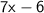
Hence, the simplified answer is 7x - 6.

Answer 2

7x - 6

General Formulas and Concepts:

Pre-Algebra

• Distributive Property

Algebra I

• Combining Like Terms

Explanation:

Step 1: Define

5x + 2(x - 3)

Step 2: Simplify

1. Distribute 2: 5x + 2x - 6
2. Combine like terms: 7x - 6