Question

Please solve this If you can thank U ​

Answer 1

`\huge{ \boxed{ \tt{1 }}}`

❁ Question : Simplify :

• 
  `\sf{( {x}^(a) ) ^(b - c) * ( {x}^(b) ) ^(c - a) * ( {x}^(c) )^(a - b)}`

❁ Solution :

First , Use power law of indices.

Remember : If
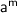`\sf{ {a}^(m) }` is an algebraic term , then

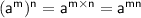`\sf{( {a}^(m) ) ^(n) } = {a}^(m * n) = {a}^(mn)` , where m and n are positive integers.

➝
`\sf{ {x}^(a(b - c)) * {x}^(b(c - a)) * {x}^(c(a - b))}`

➝
`\sf{ {x}^(ab - ac) * {x}^(bc - ba) * {x}^(ca - cb)}`

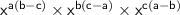
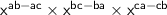
Now , Use product law of indices :

Remember : If
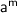`\sf{ {a}^(m) }` and
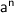`\sf{ {a}^(n)}` are the two algebraic terms , where m and n are the positive integers then
`\sf{ {a}^(m) * {a}^(n) = {a}^(m + n)}`

➝
`\sf{ {x}^(ab - ac + bc - ba + ca - cb)}`

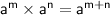
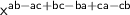
Since two opposites adds up to zero , remove them :

➝
`\sf{ {x} \: ^{ \cancel{ab} \: - \cancel{ac} \: + \cancel{bc} \: - \cancel{ba} \: + \cancel{ca} \: - \cancel{cb} } }`

➝
`\sf{ {x}^(0) }`

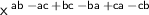
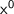
Use Law of zero index

Remember : If
`\sf{ {a}^(0)}` is an algebraic term , where a ≠ 0 , then
`\sf{ {a}^(0) = 1}`

➝
`\boxed{ \sf{1}}`

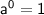
And we're done !

Hope I helped ! ♡

♪ Have a wonderful day / night ツ

~~

Answer 2

Answer:

Step-by-step explanation:

I’m not entirely sure if it’s the right answer but please have a look